Passage

Memory limit: 32 MB

A team of Byteholers has set out on a trip into Bytemountains. Unfortunately they have caused an avalanche and now have to escape it. There is an old cable-bridge over a chasm ahead of them. They have to cross the bridge as quickly as possible. The Byteholers are intimate friends and therefore have decided that either all or none of them shall survive.

The bridge is old and worn-out, so it won't withstand a great weight. The total weight of Byteholers on the bridge at any time cannot exceed some limit. Furthermore it is a cable-bridge, so the Byteholers have to cross it in groups. Next group may enter it only after the previous one has left.

It is known how much time each Byteholer needs to cross the bridge. A crossing time of a group is the crossing time of the slowest member of the group. Total crossing time of all Byteholers is the sum of crossing times of all groups. Obviously it depends on the manner in which they split into groups.

Be their saviour! Calculate the minimal crossing time of all the Byteholers.

Task

Write a programme that:

• reads the description of the bridge and Byteholers from standard input,
• determines the minimal total crossing time of all Byteholers,
• writes the determined time to the standard output.

Input

The first line of the standard input contains two integers separated by a single space: 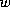- defining the maximal weight allowed for the bridge (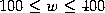) and - the number of Byteholers (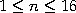). In each of the following lines there are two integers separated by a single space, describing successive Byteholers: 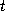- the time needed by the Byteholer to cross the bridge (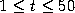) and 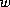- the weight of the Byteholer ().

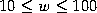Output

Your programme should write a single integer in the first and only output line. The integer should denote the minimal total crossing time of all Byteholers.

Example

For the input data:

100 3
24 60
10 40
18 50

the correct result is:

42

Task author: Piotr Stanczyk.